

Informatikseiten von Robert Löwenberg
Rotationsschablonen-Fleißner Chiffre
Das Fleißner Chiffre ist ein berühmtes Beispiel für das Gitterverfahren. Das Verfahren wurde ursprünglich von dem österreicher Eduard Fleißner
von Wostrowitz 1881entwickelt. 1885 griff Jules Verne in seinem Roman Mathias Sandorf die Idee wieder auf. In diesem Roman nam ein Mann
namens Sarcany einer erschöpften Brieftaube eine Nachricht ab, welche an drei Verschwörer gegen die Regierung adressiert war,
er versuchte diese zu entschlüsseln.
Erst drohte sein Vorhaben zu scheitern, doch Sarcany kam in Besitz der rechts zu sehenden Schablone, mit der er
die Zeichenfolge bestimmen konnte.

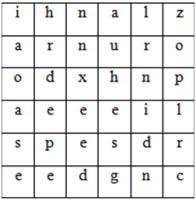
Sarcany schrieb also den ersten Teil der verschlüsselten Nachricht wie links abgebildet
auf und legte anschließend die Schablone darüber (rechts zu sehen). Anschließend drehte
er die Schablone um 90° und schrieb sich die Zeichenketten auf. Das tat er bei den anderen
zwei Teilen der Nachricht ebenfalls.

Anschließend reihte er seine vorher erhaltene Zeichenfolge hintereinander auf und erhielt folgendes:
hazrxeirgnohaledecnadnepednilruopessamnetnorevelessuotetseirtedzerrevnesuonsuoveuqlangisreimerpuater
ptsetuot
Er erkannte, dass man die Nachricht rückwärts lesen musste, denn so ergab sie Sinn: „ Tuot est prêt. Au premier signal que bous nous enverrez
de Trieste, tous se leveront en masse pour l'in dépendance de la Hongrie. Xrzah.“.
Dies bedeutete übersetzt: „Alles ist bereit. Beim ersten Zeichen, welches Sie uns von Triest aus senden werden, werden sich alle in Massen über
die Unabhängigkeit Ungarns erheben. Xrzah.“
Einführung in das Thema
Der Algorithmus
Als erstes wählt man eine Rastergröße, welche groß genug ist, alle Buchstaben des Klartextes aufzunehmen. Das klassische Fleißner Quadrat
misst 6x6 Zeichen, also passen hier insgesamt 36 Zeichen hinein. Beinhaltet der Klartext mehr Zeichen wird also einfach die Matrix vergrößert.
Danach berechnet man die Anzahl der Löcher die man benötigt. Da es vier Ablesepositionen gibt ist die Anzahl der Löcher die Klartextlänge
geteilt durch vier. Eine andere Möglichkeit ist es, die Zeichenlänge an der Kante der Matrix in das Quadrat und anschließend durch vier zu
rechnen. So bekommt man die maximale Anzahl der Löcher heraus. Wichtig ist im Weiteren die Position der Löcher, es muss unbedingt
darauf geachtet werden das in den vier Ablesepostionen jedes Loch nur einmal verwendet wird, da man keine Buchstaben übereinander
schreiben kann. Dies kann man beim Erstellen der Schablone zum Beispiel dadurch erreichen, dass man ein Feld als Lücke wählt und danach
alle Felder markiert, die beim Drehen dieser Lücke vorkommen.
Anschließend legt man die Schablone auf eine leere Matrix und schreibt den Klartext in die Löcher. Sind alle Löcher vorerst gefüllt, wird diese
gedreht und es werden die Löcher gefüllt. Nun dreht man die Schablone zwei weitere Male. Ist der Klartext fertig verschlüsselt, obwohl noch
Löcher frei sind, werden diese mit sogenannten Blendern gefüllt, also zufälligen Buchstaben.
Dechiffriert wird, indem man die Schablone auf das Quadrat legt, und nun die Buchstaben aus den freien Feldern abliest. Man dreht die
Schablone nun weitere drei Mal ja nach Art in Uhrzeigersinn oder gegen Uhrzeigersinn, und sollte dann den kompletten Klartext erhalten.
Entweder bekommt der Empfänger die Schablone oder aber einen Schlüssel, welcher aus Ziffern besteht und beispielsweise so angegeben
wird : 4 5 10 15. In Form einer Schablone würde das dann wie folgt aussehen, man liest die Ziffern von links nach
rechts und von oben nach unten (weiß sind die Löcher):

Meine Beispiele
Folgendes Zitat gilt es im Uhrzeigersinn zu ver-und entschlüsseln:
Der Gescheitere gibt nach! Eine traurige Wahrheit, sie begründet die Weltherrschaft der Dummheit.
Als erstes machen wir uns Gedanken über die Größe der Matrix. Ohne Leerzeichen beträgt der Plaintext eine Zeichenanzahl von 86.
Das heißt eine 9x9 Matrix wäre zu klein (9*9=81, wir brauchen aber 86), also nehmen wir eine Matrix in der Größe von 10x10. So
könnten wir theoretisch bis zu 100 Zeichen chiffrieren. Da wir 100 Zeichen chiffrieren könnten und vier Ablesepositionen haben,
kann unsere Schablone bis zu 25 Löcher fassen. Wir überlegen uns ein sinnvolles Muster, so dass es keine doppelten Buchstaben
gibt.

Ich hab mir dazu diese ausgedacht, natürlich gibt es mehrere Möglichkeiten:
Als nächstes nehmen wir uns diese Schablone, legen diese auf die leere 10x10 Matrix und beginnen in die Löcher unseren Plaintext
zu schreiben:
Sind alle Lücken vorerst gefüllt drehen wir die Schablone nun noch drei mal um jeweils 90°, insgesamt 4. Mal.
2. Mal
3. Mal
4. Mal-restliche Lücken werden mit Blendern aufgefüllt
1. Mal
Nun entfernen wir die Schablone. Die noch freien Stellen können nun durch zufällige Buchstaben (Blendern) ersetzt werden. Am Ende erhalten
wir folgendes Chiffrat:
Ein weiteres Beispiel
Plaintext: Zukunft ist etwas, was zu erreichen jedermann sechzig Minuten in der Stunde
braucht - was immer er tue wer immer er sei. (C.S. Lewis)
Zeichen ohne Leerzeichen 112 à 12x12 Matrix (144 Zeichen) à geteilt durch 4 (Ableserichtungen) = 36 Löcher
Nun werde ich nicht mehr jeden Schritt einzeln erklären, da das Prinzip oben zu entnehmen ist.

Als Schablone nehmen wir also folgende:
Als nächstes Füllen wir wieder die Löcher in der Matrix mit Buchstaben aus. So entsteht folgendes:
Um den optischen Eindruck zu verbessern habe ich die Schablone diesmal schwarz gehalten.








Sind alle Lücken vorerst gefüllt drehen wir die Schablone nun wieder drei mal um jeweils 90°, insgesamt also 4. Mal.

2. Mal
Und das ist unser fertiges Chiffrat:

Entschlüsselung:
Verschlüsseln:
Wir legen nun nur die Schablone auf das Chiffrat und schon kann das entschlüsseln beginnen. Wenn wir die ersten Buchstaben aus den Löchern
übernommen haben. Drehen wir nun die Schablone weitere 3 Mal bis wir nun unseren vollständigen Plaintext haben.
Entschlüsselung:
Wir legen nun nur die Schablone auf die Matrix und schon kann das entschlüsseln beginnen. Wenn wir die ersten Buchstaben aus den Löchern
übernommen haben. Drehen wir nun die Schablone weitere 3 Mal bis wir nun unseren vollständigen Plaintext haben.
Verschlüsselung:
Und nun.. Viel Spaß beim ausprobieren! Ich hoffe ich konnte euch das Fleißner-Chiffre näher bringen!
Im Anschluss noch meine Quellen:
•
https://de.wikipedia.org/wiki/Fleißnersche_Schablone
•
https://www.kryptographiespielplatz.de/index.php?aG=6a74ce6c9e2398be3cca10d25177e00ca450a1e1
•
http://kryptografie.de/kryptografie/chiffre/fleissner.htm
•
http://www.mathe.tu-freiberg.de/~hebisch/Praktikum10-2/Gitter-Verfahren/Gitter-Verfahren.html
•
http://matheplanet.com/default3.html?call=viewtopic.php?topic=182494&ref=https%3A%2F%2Fwww.google.de%2F













